Breaking the magnetic resonance imaging acquisition speed barrier: Clinical implications of parallel imaging

Dr. Sodickson is currently a 4th-year Radiology Resident at Brigham and Women's Hospital, Boston, MA. He earned his BS in Physics from the Massachusetts Institute of Technology, his PhD in Medical Physics from the Harvard-MIT Division of Health Sciences and Technology, and his MD from Harvard Medical School.

Parallel imaging has recently emerged as a powerful new approach to magnetic resonance imaging (MRI) acquisition that enables significant reductions in acquisition time. While a variety of different techniques have emerged, the common principle behind all of them is to use the spatial information inherent in the elements of a radiofrequency (RF) coil array to allow a reduction in the number of time-consuming phase-encode steps required during the scan. These techniques may be applied to any existing pulse sequence, and, in their simplest implementations, can be used to reduce imaging time at fixed resolution, or, alternatively, to increase resolution at fixed imaging time. The savings in imaging time can, however, be applied toward a variety of other ends as well.

This article summarizes some of the fundamental principles, the practical operational requirements, and the developing clinical applications of parallel MRI techniques. The basic mechanisms of spatial encoding in parallel acquisitions are reviewed, along with the associated tradeoffs in signal-to-noise ratio (SNR). Pulse sequences and acquisition strategies that are particularly synergistic with parallel imaging are described. After a survey of the broad range of clinical studies that benefit from typical levels of acceleration, the frontiers of parallel imaging development are explored, including order-of-magnitude accelerations for volumetric imaging, and combinations with high-field MRI.

 

Review of traditional spatial encoding in magnetic resonance imaging

Since the beginning of MRI, spatial encoding has generally been achieved by taking advantage of the spatially dependent evolution of nuclear spins (typically protons) in an externally applied magnetic field gradient to fill a plane or a volume of k-space, which is then Fourier- transformed to produce the two-dimensional (2D) or three-dimensional (3D) image matrix. Spatial localization along the frequency-encode direction is quite rapid, and is determined by the local precession frequency as signal is collected in the presence of the readout gradient.

Spatial encoding along the orthogonal phase-encode direction is much more time consuming, and accounts for the lengthy acquisition times encountered in traditional imaging methods. Evolution under phase-encoding gradients is determined by numerous repetitions of the pulse sequence with incremented phase- encoding gradient steps, each incurring an additional repetition time (TR). Traditionally (in the absence of half-Fourier techniques), this requires a number of phase-encode repetitions equal to the phase-encode matrix size, and results in long examination times.

In 2D acquisition techniques, individual slices are imaged separately after excitation by an RF pulse in the presence of the slice-select gradient. A full plane of k-space is filled by the acquired signal, and Fourier-transformed to produce the individual image slice. In contrast, 3D techniques excite the entire image volume at once, and spatially encode along the "slice direction" as well with additional phase-encode steps, resulting in a 3D volume of signal that is Fourier-transformed along all 3 dimensions to produce the full volumetric image matrix.

Radiofrequency coils with nearly uniform sensitivity over the imaging volume (eg, the prototypical body coil) are often used to image large volumes. For focused imaging of smaller volumes, numerous surface coil designs exist, which have higher sensitivity in defined regions of interest. Coil arrays, or so-called "phased array coils," combine the benefits of the increased SNR of the individual component coil elements with the larger coverage area of their combination. In traditional use, multiple receiver systems separately collect the signal from each of these coil array elements, and a composite image is formed as the square root of the sum of squares of the individual images, as this conveniently approximates the highest achievable overall SNR. ¹

 

Basic principles of parallel
imaging techniques

After a number of early proposals ^2-5 of ways to use multiple RF coils to increase data acquisition speeds in MRI, the field of parallel imaging for clinical use first blossomed with the introduction of the SMASH (SiMultaneous Acquisition of Spatial Harmonics) technique. ⁶ This was soon followed by the SENSE (SENSitivity Encoding) technique, ⁷ and subsequently by a wide variety of related hybrid and generalized approaches. ^8-11

All of these methods use spatial variations in the coil sensitivities of the individual array elements to take the place of time consuming phase-encoding gradient steps. By using combined spatial encoding with both gradients and coil sensitivities, these techniques allow reduced sampling densities in k-space, which correspond to aliased images in the spatial domain. Parallel imaging reconstructions use knowledge of the spatial behavior of the individual coil sensitivities to reconstruct the intervening lines in k-space in these under-sampled data sets, or equivalently, to unfold aliased pixels within the corresponding aliased images. The number of slow, serial phase-encode steps that comprise the temporal bottleneck in MR imaging is decreased, resulting in increased imaging speed.

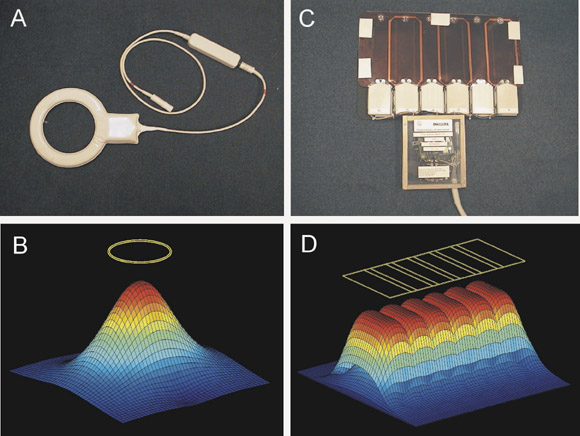
An individual wire loop or coil array element has a spatially localized coil sensitivity (Figure 1A and 1B), which determines the portion of the imaging volume from which it is capable of collecting signal. An array of such elements (Figure 1C and 1D) produces separate coil sensitivities spatially displaced along the length of the array. Each individual element effectively "sees" a different portion of the imaging volume, and samples the target magnetization density shaded by its own coil sensitivity function. If the coil is appropriately aligned along the phase-encode direction, then this spatial information may be exploited to allow for a decreased amount of gradient encoding.

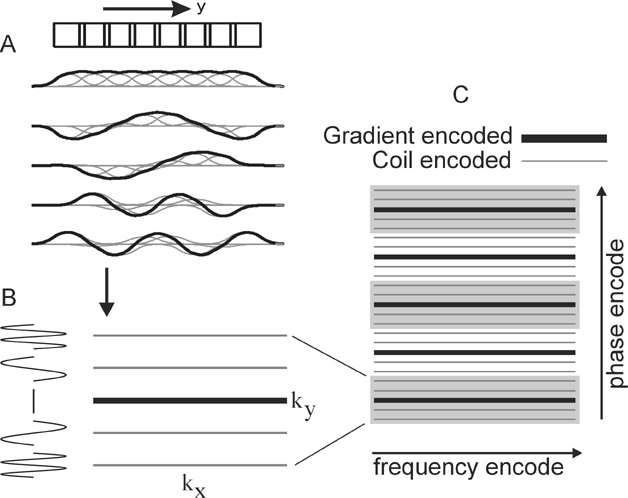
Two intuitive pictures are helpful to understand the image reconstruction approaches of parallel imaging. The k-space picture exemplifies the original SMASH technique. ⁶ Figure 2A shows that appropriate linear combinations of the coil sensitivity functions may be produced to simulate sinusoidal variations in signal across the image plane. In this schematic example, summing the signal from all coils produces a nearly uniform sensitivity, while adding or subtracting the signal from adjacent coils in appropriate combinations produces an overall signal modulated by sinusoids of varying spatial frequencies. As evolution in the phase-encoding gradient normally produces sinusoidal variations in magnetization across the image volume, these combinations of signals from the elements of a coil array may thus be used to mimic the effects of phase-encode gradient steps. This allows for a decreased number of phase-encoding steps, with the omitted lines in k-space filled in by appropriate signal combinations (Figure 2B and 2C).

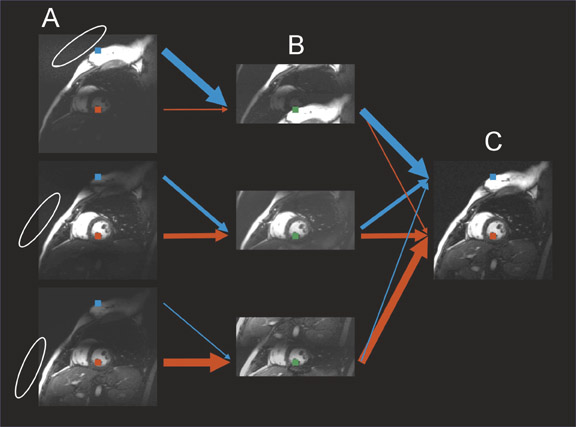
The image domain picture exemplifies the original SENSE technique. ⁷ As shown in Figure 3A, each coil array element effectively samples a different portion of the imaging volume, producing an image shaded by its coil sensitivity. By undersampling k-space along the phase-encode direction, aliased images are simultaneously acquired from each coil (Figure 3B). Each aliased pixel is composed of a linear combination of source pixels weighted by the coil sensitivity of the array element at those source pixel locations. Knowledge of the values of the coil sensitivities at all positions allows a mathematical unfolding of the aliased pixels to produce the full image without aliasing (Figure 3C).

Conceptually, there is equivalence of the k-space and image domain pictures: Acquisition of undersampled k-space data for each coil results in individual aliased images, and reconstruction of the full image requires one to fill in the missing lines of k-space, or equivalently, to "un-alias" the aliased images. The numerous reconstruction techniques that have been introduced differ largely in the specifics of their reconstruction algorithms and the mathematical constraints applied. However, they may all be understood as combinations of the intuitive k-space and image domain pictures. The final images produced with the different methods are not necessarily identical but may vary somewhat in the nature of any residual aliasing artifacts, and in the details of the noise profile across the image.

Figures 2 and 3 show one-dimensional accelerations performed along traditional Cartesian axes, with the coil array aligned along the phase-encode direction. Analogous techniques may be used to separate image data from different slices that have been excited simultaneously. ^12,13 Alternatively, parallel imaging may be performed along both phase-encode directions in 3D acquisitions, for bidirectional, multiplicative acceleration factors. ¹⁴ These approaches may also be generalized to non-Cartesian trajectories such as undersampled spiral and radial acquisitions. ^15-18 Non-Cartesian k-space trajectories result in more complex aliasing patterns and underfilling of k-space, resulting in increased computational complexity of the image reconstruction.

 

Impact on signal-to-noise ratio

As in most MRI techniques, the decreased imaging time in parallel MRI studies typically incurs a penalty in SNR. SNR is degraded in parallel imaging by two fundamental mechanisms. A general principle of MR signal acquisition is that each acquired point in k-space adds signal coherently while averaging the incoherent noise. Reducing the number of acquired phase-encoded k-space lines by an acceleration factor, R, thus causes a decrease in the net SNR by a factor ÖR. In addition, all parallel imaging reconstruction algorithms introduce an additional noise amplification factor or geometry factor, g. This g factor is always >1 and is spatially dependent in a manner determined by the coil array geometry, the imaging volume, and the details of the reconstruction algorithm used. ^7,19 The g factor also increases in a complex fashion with higher values of the acceleration factor R. The net SNR is thus as follows:

 

SNR = SNR _full

gÖR

 

where SNR _full refers to the SNR of a corresponding unaccelerated image. Given this expected degradation in SNR, the most natural applications of parallel imaging involve studies in which there is SNR or contrast-to-noise ratio (CNR) to spare, such as contrast-enhanced MR angiography (CE-MRA), or volumetric acquisitions that boost SNR by acquiring signal from the entire image volume at once rather than sequentially from each slice.

 

Operational requirements

Knowledge of the individual coil sensitivity functions must be obtained to perform any parallel imaging reconstruction, as this will allow the appropriate linear combination of signals to reconstruct the omitted k-space lines or to unfold the aliased images. Any errors in the coil sensitivity estimates may result in residual aliasing artifacts. Sensitivity maps may be obtained from low resolution pre-scans of the patient with the coil array in place. Alternatively, a number of autocalibrating techniques have been developed that acquire enough extra data during the scan itself to extract the sensitivity profiles. ^11,20-22 The simplest such techniques acquire the center of k-space in its entirety to serve as the sensitivity maps, which are then used to fill in the undersampled periphery of k-space. These autocalibrating techniques are particularly beneficial in settings where patient or organ motion is present, as any variations in sensitivity profiles are intrinsically updated throughout the imaging session.

Parallel imaging imposes particular hardware requirements. Coil arrays must be used, with separate preamplifiers and receivers for each individual element, and appropriate decoupling networks to decrease crosstalk between elements. Parallel imaging techniques may be used with existing coil arrays, but many tailored array geometries have also been designed specifically with parallel imaging in mind for better results. ^23-26

Recently, the three major vendors of MR scanners have all implemented versions of parallel imaging in their commercial systems. Philips scanners (Philips Medical Systems, Best, The Netherlands) incorporate 6 separate receivers, and use a SENSE reconstruction. Siemens systems (Siemens Medical Solutions, Erlangen, Germany) typically have 4 receivers, with some 8 receiver systems available, and use iPAT (integrated Parallel Acquisition Technology) with a choice of a self-calibrating SENSE-like and a self-calibrating SMASH-like (GRAPPA, ¹¹
GeneRalized Autocalibrating Partially Parallel Acquisition) reconstruction. General Electric (GE Medical Systems, Milwaukee WI) has both 4 and 8 receiver systems, and currently performs parallel imaging with ASSET (Array Spatial and Sensitivity Encoding Technique), a SENSE-
like reconstruction.

While operational details vary from vendor to vendor, a scan performed with parallel imaging techniques typically involves choosing and positioning an appropriate coil array, specifying the acceleration factor, and either performing a sensitivity calibration at some point during the examination or using a vendor's self-calibrating approaches. The parallel imaging reconstructions are then performed automatically on these commercial systems to produce full, unaliased images by appropriate manipulation of the data gathered from each of the individual coil elements.

 

Options for using increased
imaging speed

Perhaps the most obvious application of parallel imaging is to decrease the acquisition time with fixed resolution and imaging parameters. This approach may be used to shorten breath-hold durations, to increase anatomic coverage in a fixed scan time, or to increase patient throughput. It may be used to increase temporal resolution, particularly for dynamic techniques such as cardiac imaging, ^27,28 and time-resolved MRA. ^29,30 Alternatively, parallel imaging may be used to increase image matrix and spatial resolution in a fixed scan time. ³¹ It may be used to improve image quality, for example by decreasing T2 blurring effects from long echo trains in Fast Spin-Echo (FSE), Turbo Spin-Echo (TSE), or single-shot sequences. ³¹ The shortened acquisition times can decrease artifacts secondary to patient motion, susceptibility and chemical shift effects. In certain circumstances, pulse sequences may even be optimized to increase SNR, despite the inherent SNR losses of faster acquisition times and g factor. This may be achieved, for example, by using decreased bandwidth, increased repetition time, and increased flip angle during a gradient-echo sequence. ³² Faster scan time in CE-MRA may support an increased rate of contrast injection to boost CNR. Other applications making use of parallel imaging for more than mere speed have also been described: for example, a number of techniques have been developed using parallel imaging techniques for detection and correction of motion or other artifacts. ^33-35

 

Clinical applications of parallel imaging

Parallel imaging has been applied across a wide variety of organ systems and examination types. ³⁶ Although, it is impossible to discuss or reference all of them here, an effort has been made to include many of the seminal initial works, along with a sampling of compelling recent examples.

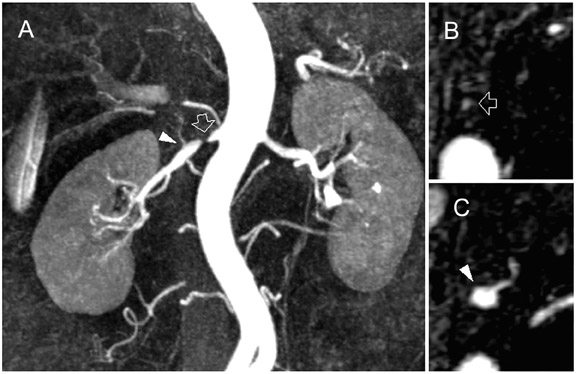
Contrast-enhanced MR angiography is a particularly attractive application, in part due to the intrinsically high CNR from contrast administration. The time savings of parallel imaging may be used to advantage in MRA to increase resolution in a given imaging time, or to increase temporal resolution in the move toward time-resolved angiography, thus diminishing concerns of missing the contrast bolus, or of venous contamination. These benefits have been shown in MRA of the aorta and visceral vessels, ^29,30 carotid MRA, ³⁷ and peripheral MRA. ^38,39 Figures 4 and 5 show examples of renal and peripheral vascular MRA, with combinations of speed and spatial resolution that would not have been achievable without parallel imaging.

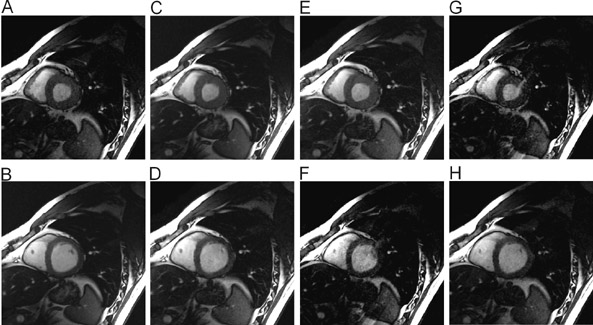
Significant efforts have been made toward improving cardiac MRI with parallel imaging. ^27,28 Intuitively, the faster acquisition speeds may lessen some of the challenges of imaging this moving target. As shown in Figures 6 and 7, applications to cardiac imaging have ranged from coronary imaging, ⁴⁰ which benefits from increased resolution in a given imaging time, to functional and real-time cardiac imaging, ⁴¹ for which temporal resolution is of the essence.

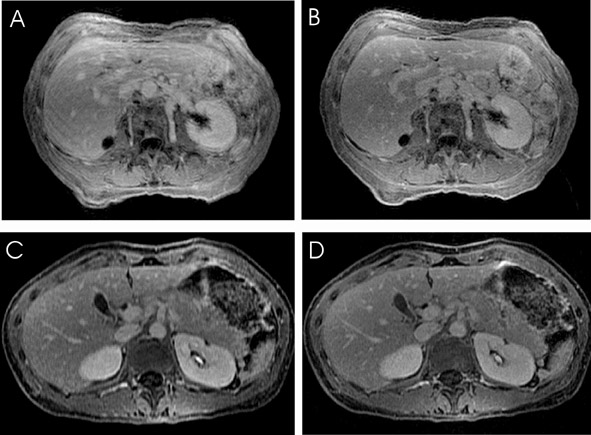
Abdominal imaging applications (Figure 8) stand to improve significantly from parallel imaging techniques. Faster acquisition may be applied toward increasing anatomic coverage in a given breath-hold, or reducing breath-hold lengths to diminish respiratory or other motion artifacts. ⁴² Alternatively, time savings may be used to increase resolution for better visualization of small lesions. ⁴³ Benefits to breast imaging have been shown both by increasing temporal resolution in dynamic imaging, ⁴⁴ and by permitting simultaneous examination of both breasts with standard single-breast resolution. ⁴⁵ The challenges of imaging the moving fetus make fetal MRI an area ripe for the application of parallel imaging techniques.

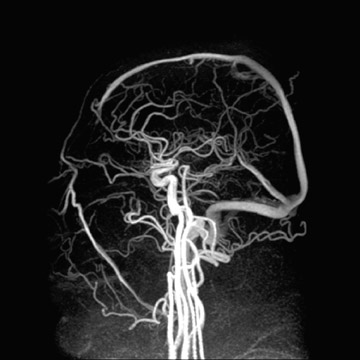
Applications to neurologic imaging are also on the rise. Imaging accelerations have been applied to spectroscopy, ^46.47 diffusion-weighted imaging (DWI), ⁴⁸ diffusion tensor imaging and white matter tractography, ^49,50 and functional MRI (fMRI). ^51-53 Figure 9 shows a high CNR phase-contrast MRA of the brain in a scan time made feasible only by the application of parallel imaging accelerations. ⁵⁴ Benefits at higher field strengths of 3T to 7T are quite promising to the future of high-field neuroimaging as well. Significant reductions in susceptibility artifacts at high field have been shown, as Figure 10 illustrates for echoplanar DWI at 3T. ⁵⁵

 

Pushing the limits

For conventional coil array designs and typical imaging volumes, the noise amplification g factor can rise prohibitively as the acceleration factor increases. As a result, typical accelerations along one dimension generally do not exceed a factor of 4. It has been shown, however, that accelerations may be performed along both phase-encode axes of a 3D acquisition with significantly lower g factors for equivalent accelerations. ¹⁴ Recently, order-of-magnitude accelerations have first been shown for volumetric, CE-MRA of the thoracic and abdominal aorta. ⁵⁶ These images were acquired at 1.5T, with a prototype 32-receiver system (GE Global Research Center, Niskayuna, NY) and a 32-element clamshell coil array with 16 elements each above and below the patient. Three-fold acceleration was used in the craniocaudal direction, and 4-fold acceleration was used transversely, for a combined acceleration factor of 12. These high acceleration factors make possible the acquisition of a large image volume at high spatial and temporal resolution. Figure 11 shows a time-resolved approach, with the entire 36 * 36 * 36 cm image volume acquired dynamically every 4.5 seconds (reduced from the 54 seconds that would have been required with a conventional acquisition). A higher resolution approach with lower temporal resolution was also described, utilizing 22 second volumetric breath-hold acquisitions (reduced from 4.4 minutes). The large coverage volumes used in both these approaches easily include the full arterial anatomy of the abdomen in a single acquisition, including the entire celiac axis and superior mesenteric artery territories anteriorly, the renal arteries and inferior mesenteric artery, and even the gluteal branches of the internal iliac arteries posteriorly.

These examples underscore the synergy of volumetric acquisition with parallel imaging. Without the acquisition speeds of parallel imaging, large volume 3D scans would not be possible in a single breath-hold. Conversely, the increased SNR of volumetric scanning enables high acceleration factors by compensating for the SNR losses incurred by decreased acquisition times and the g factors of parallel imaging techniques. The resulting acquisition speeds may rival those of multidetector CT, or provide the time-resolved benefits of conventional angiography, while at the same time permitting the full range of tissue contrast mechanisms unique to MRI.

The recent advent of higher field systems ranging from 3T to 7T will provide further synergy with parallel imaging techniques. The increased baseline SNR will enable more widespread use of parallel imaging, and the increased RF focusing ability (the narrower spatial extent of the RF field for a given coil geometry) at higher frequency is beneficial for improved reconstructions. ^57,58 Parallel imaging also holds great promise in enabling higher field work, and can easily be implemented to decrease RF power deposition or specific absorption ratio (SAR) by reducing the length and/or the density of echo trains, to decrease acoustic noise by reducing the amount of required gradient switching, ⁵⁹ and to reduce susceptibility artifacts (Figure 10) that become increasingly troublesome with increasing field strength.

 

Conclusion

Parallel imaging techniques provide a powerful new set of tools for use in clinical MRI. Recent technical advances and increased availability to imaging centers place parallel imaging at the cusp of widespread clinical use. Increased speeds do come at a well-defined cost in SNR, which must be taken into account in the planning of imaging protocols. However, for applications with sufficient baseline SNR, parallel MRI can offer substantial benefits. There is great synergy both with 3D volumetric acquisitions and with high-field MR systems. As experience with these techniques grows, the future of clinical MRI may well shift toward rapid, volumetric acquisitions. Just as the advent of multidetector CT scan-ners spurred an explosion of imaging improvements, parallel imaging techniques promise to enable a broad range of new clinical MR applications.

 

Acknowledgments

It has been a source of great pleasure to watch my brother Dr. Daniel Sodickson's work evolve over the past several years, and to see the techniques of parallel imaging expand from the research realm into clinical practice. I thank him for the use of several images, and for many enjoyable conversations on the finer points of parallel MRI. Many thanks are due Dr. Frank Rybicki, for his mentorship in this project and for his editorial assistance. I am most grateful to Drs. Charles McKenzie, Neil Rofsky, Stefan Schönberg, Jeffrey Maki, Thoralf Niendorf, Johan van den Brink, Romhild Hoogeveen, and Christiane Kuhl, all of whom kindly contributed samples of their work for reproduction here.